Vanishing Points and “Gaussian Sphere Representation”

Vanishing points are an important concept in 3D vision. Many papers related to them are using a notation called Gaussian sphere representation, which I find hard to understand at the beginning. This document will summarize what vanishing points (and their “Gaussian sphere representation”) are, how to represent them, what information they encode, how to find them, and why they are useful.

WARNING: This article is for people who want to learn more about vanishing points. Basic knowledge in 3D vision is assumed (e.g., you know the existance of camera calibraion (intrinsic) matrices).

Introduction

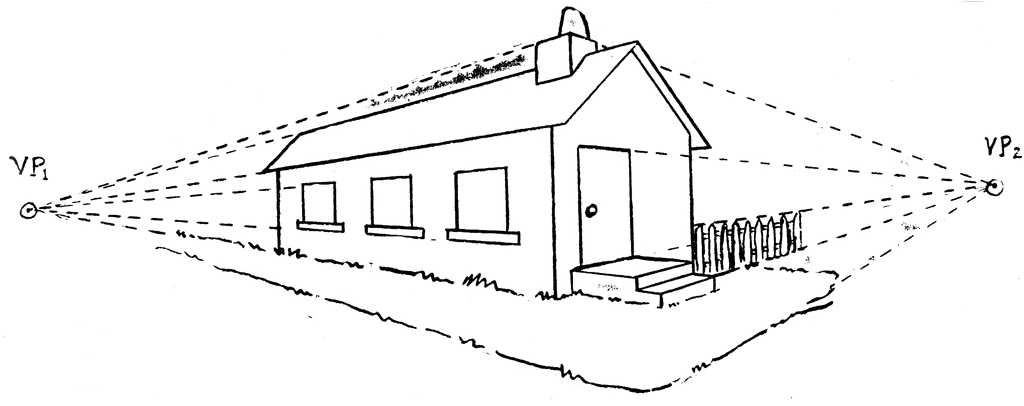
With perspective geometry, all 3D parallel lines will intersect at the same point in 2D at their vanishing points when they are projected to an image. To see this, we can write down the equation of a 3D ray. Any point on a ray can be represented with \(\textbf{o}+\lambda \mathbf{d}\), in which \(\bf o\) is the origin and \(\mathbf{d}\) is the direction of the line. Let \(K\) be the camera calibration matrix, we have its 2D projection being

\[ z \begin{bmatrix} p_x\\p_y\\1 \end{bmatrix} = K \cdot (\mathbf{o}+\lambda \mathbf{d}). \]

The vanishing point \(\bf p\) is defined to be the projection of a line at infinity. To find where \(\bf p\) is, we set \(\lambda \to \infty\). The contribution of \(\textbf{o}\) to the projection point \(\bf p\) then becomes negligible. Therefore the vanishing point \(\mathbf{p} \sim K \cdot \mathbf{d}\) is uniquely determined by the line direction \(\mathbf{d}\).

The above derivation also tells us that if we can detect the vanishing point \(\bf p\) in an image, we can compute the direction \(\mathbf{d}\) of those parallel lines in 3D! Isn't it amazing that we can infer the 3D information from single 2D images? In the next section, I will present an elegant and numerically stable way to compute \(\bf d\) from two 3D parallel lines.

Gaussian Sphere Representation for Vanishing Points

Now let us say you have two parallel lines \(\ell_1 \mathbin{\!/\mkern-5mu/\!} \ell_2\) in 3D, whose endpoints are \((u_{1},u_{2})\) and \((v_{1},v_{2})\) when projected to the image plane \(z=1\), assuming a calibrated camera. Let the camera position \(o=(0,0,0)\). Then the normals of \(\triangle ou_{1}u_{2}\) and \(\triangle ov_{1}v_{2}\) are

\[ \begin{align} \mathbf{n}_{u} &= u_{1}\times u_{2}\\ \mathbf{n}_{v} &= v_{1}\times v_{2}. \end{align} \]

Any lines in the plane \(\triangle ou_{1}u_{2}\) must be orthogonal to its normal \(\mathbf{n}_{u}\). The same applies to the lines in the plane \(\triangle ov_{1}v_{2}\). Let \(\mathbf{d}\) be the direction vector of parallel line \(\ell_1\) and line \(\ell_2\). This orthogonal condition means that \(\mathbf{n}_{u} \perp \mathbf{d} \perp \mathbf{n}_{v}\), so we have

\[ \mathbf{d}=\mathbf{n}_{u}\times \mathbf{n}_{v}. \]

In addition, the intersection of \(\mathbf{d}\) with image plane \(z=1\) is also the intersection point \(\bf p\) of line \((u_{1},u_{2})\) and line \((v_{1},v_{2})\) (read introduction section again if you do not understand this). Traditionally, the intersection point $\bf p$ (in the image space) is referred as the vanishing point, while the direction vector \(\mathbf{d}\) is called the Gaussian sphere representation of the vanishing point (IMHO a confusing name).

You can see that the vector \(\mathbf{d}\) is indeed a better representation compared to using the intersection point on the image plane. First, if \(\mathbf{d}\) does not intersect with the focal plane at all, e.g., when it is vertical, the vanishing point \(\bf p\) will be near the infinite, which is ill-condition. Second, it is hard to define a metric to measure the distance between two vanishing points. The common-used Euclidean distance is not a good metric if the camera calibration is known. With the direction vector \(\mathbf{d}\), we can use the angle between them

\[ D\left(\mathbf{d}_{1},\mathbf{d}_{2}\right)=\left\langle \frac{\mathbf{d}_{1}}{\left\Vert \mathbf{d}_{1}\right\Vert },\frac{\mathbf{d}_{2}}{\left\Vert \mathbf{d}_{2}\right\Vert }\right\rangle \]

as a more reasonable distance metric.

Vanishing Point Detection

Here, I give a RANSAC-based vanishing point detection algorithm that works with the Manhattan scenes, i.e., scenes with three orthogonal vanishing points, when the camera calibration is known. The algorithm starts with a set of detected 2D lines that can be found with LSD and then does RANSAC:

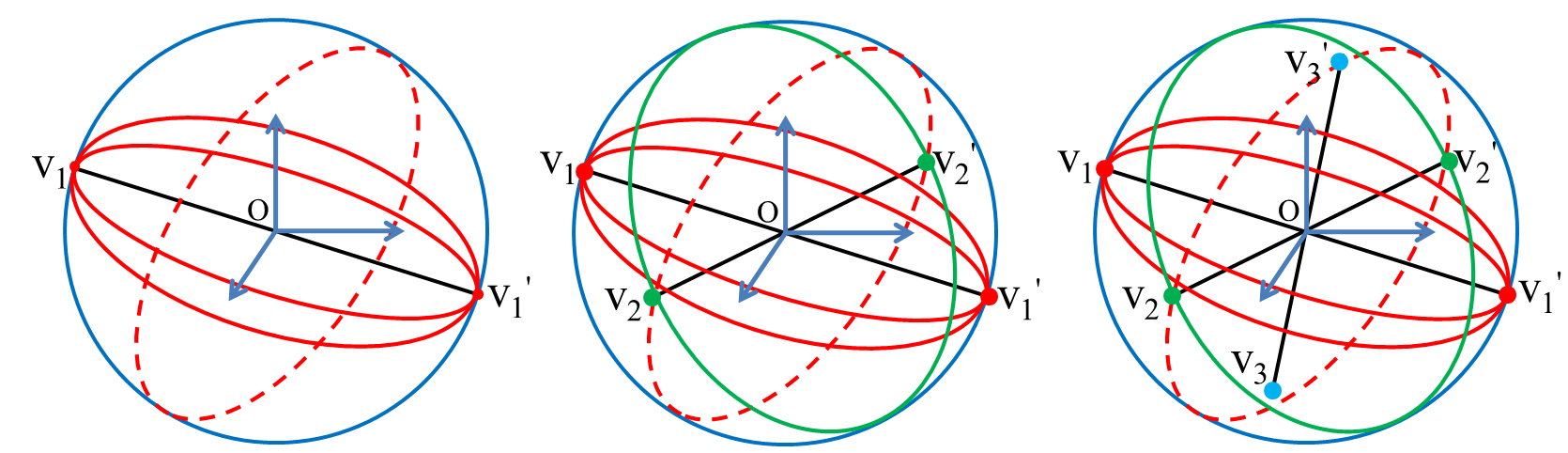
1. Random select three lines \(\ell_1\), \(\ell_2\), and \(\ell_3\). We assume that \(\ell_1 \mathbin{\!/\mkern-5mu/\!} \ell_2\) and \(\ell_1 \perp \ell_3 \perp \ell_2\) in 3D;

2. We compute the Gaussian sphere representation \(\mathbf{d}_1\) of the vanishing point for lines \(\ell_1\) and \(\ell_2\) with their endpoints using the method from previous section;

3. Compute \({\bf d}_2\) with the endpoints of \(\ell_3\). For the another line (that does not exist), we set normal of imaginary triangle \(\triangle ov_{1}v_{2}\) to be \(\mathbf{n}_v = \mathbf{d}_1\);

4. Compute \({\bf d}_3 = {\bf d}_1 \times {\bf d}_2\);

5. Check the consistency using RANSAC for vanishing points \(({\bf d}_1,{\bf d}_2,{\bf d}_3)\) with other lines;

6. Repeat 1-5 until a good set of vanishing points are found.

For scenes that are not Manhattan or the camera is not calibrated, a classic way is to use the combination of LSD + J-linkage. Readers can refer to the J-linkage clustering algorithm for more details.

Application: Photo Forensics (Camera Calibration)

Photo forensics is an art to detect whether a photo was tampered by Photoshop. In this example, we will check if a photo was cropped. This is equivalent to recovering the camera calibration matrix

\[ K=\begin{bmatrix} f & 0 & o_{x}\\ & f & o_{y}\\ & & 1 \end{bmatrix}. \]

Why \(K\) can tell us whether an image was cropped or not? This is because for common cameras and lens, the choice of the focal length \(f\) is often limited and the offset of the camera center \((o_x,o_y)\) should be around the center of the image. An image that has been arbitrarily cropped would violate those properties.

One way to recover \(K\) is from vanishing points. In order to successfully recover the camera calibration, we need to know at least three orthogonal vanishing points. Finding those vanishing points are not that hard, it requires the user to label three pair of parallel lines that are perpendicular to each other in 3D. Each pair of parallel lines uniquely determines a vanishing point. Three pair of parallel lines are easy to find in man-made environment, as objects tend to be rectangular and cuboid.

Once we know three orthogonal vanishing points, we are able to recover the camera's calibration matrix \(K\). Let our 2D lines be \((\hat{u}_{1},\hat{u}_{2})\) and \((\hat{v}_{1},\hat{v}_{2})\) in the image space, in which the \(x\) and \(y\) coordinate of those variables are the pixel coordinates and \(z\) coordinates are 1. According to the camera's perspective projection model, we have

\[ \begin{align*} z_{u_i}\hat{u}_{i} & =Ku_{i}\\ z_{v_i}\hat{v}_{i} & =Kv_{i}, \end{align*} \]

where \(u_{i}\) and \(v_{i}\) are the coordinates in the calibrated image space for \(i \in \{1,2\}\). Then the direction vector

\[ \begin{align*} \mathbf{d} & =\mathbf{n}_{u}\times \mathbf{n}_{v}\\ & =\left(u_{1}\times u_{2}\right)\times\left(v_{1}\times v_{2}\right)\\ & \propto \left[\left(K^{-1}\hat{u}_{1}\right)\times\left(K^{-1}\hat{u}_{2}\right)\right]\times\left[\left(K^{-1}\hat{v}_{1}\right)\times\left(K^{-1}\hat{v}_{2}\right)\right]\\ & \stackrel{1}{=}\left[K^{T}\left(\hat{u}_{1}\times\hat{u}_{2}\right)\right]\times\left[K^{T}\left(\hat{v}_{1}\times\hat{v}_{2}\right)\right]\\ & \stackrel{2}{=}K^{-1}\left[\left(\hat{u}_{1}\times\hat{u}_{2}\right)\times\left(\hat{v}_{1}\times\hat{v}_{2}\right)\right]\\ & =: K^{-1}\left(\hat{\bf n}_{u}\times\hat{\bf n}_{v}\right)\\ & =: K^{-1}\hat{\bf d}. \end{align*} \]

Here, \(=:\) represents “define as” and in \(\stackrel{1}{=}\) and \(\stackrel{2}{=}\) we use a useful conclusion for cross product from Yi Ma's “An Invitation to 3D Vision” Exercise 2.4:

\[ K^{-T}\widehat{\omega}K^{-1}=\widehat{K\omega} \]

when \(K\) is invertible. See Yi's Book for more details. Notice that \(\hat{\mathbf{d}}\), \(\hat{n}_{u}\) and \(\hat{n}_{v}\) are known given the lines in the pixel coordinate. Now if we have three orthogonal vanishing points \(\mathbf{d}_{1}\perp \mathbf{d}_{2}\perp \mathbf{d}_{3}\), we can write down the equation

\[ \begin{align*} \hat{\bf d}^T_{1}K^{-T}K^{-1}\hat{\bf d}_{2} & =0\\ \hat{\bf d}^T_{2}K^{-T}K^{-1}\hat{\bf d}_{3} & =0\\ \hat{\bf d}^T_{3}K^{-T}K^{-1}\hat{\bf d}_{1} & =0. \end{align*} \]

Notice that

\[ S := K^{-T}K^{-1}=\frac{1}{f^{2}}\begin{bmatrix}1 & 0 & -o_{x}\\ 0 & 1 & -o_{y}\\ -o_{x} & -o_{y} & o_{x}^{2}+o_{y}^{2}+f^{2} \end{bmatrix} \]

so that the previous three equations are linear with respective to \(o_{x}\), \(o_{y}\) and \(o_x^{2}+o_y^{2}+f^{2}\). If we have more than three vanishing points, we can do a lasso optimization to optimize the L1 norm (you can use L2 for convenience, but L1 is generally more “robust”)

\[ \min_{f,v_{x},v_{y}}\sum_{i,j}\ \left|\hat{\bf d}^{T}_{i}S\hat{\bf d}_{j}\right| \]

to find the best camera parameters.

Acknowledgement

Thanks Cecilia Zhang for the discussion about vanishing points and photo forensics. Thanks Prof. Yi Ma for the discussion about the relationship between vanishing points and camera calibration.